乒乓球运动分析与Matlab仿真

李孝锋

最近上课老师讲了一个乒乓球运动的案例，觉得挺有趣的，就在课后做了一点实践，不足之处请各位大佬批评指正。
背景介绍

网上找到一篇写的很棒的推送，深入了解的小伙伴们可以看一下，我再背景介绍和力学分析这块和部分素材也会主要采用文章的介绍展开，如有侵权，请联系删除。
喜欢打乒乓球的小伙伴都知道下旋球，落地后回旋让对手措手不及。这样的回旋运动也比较容易实现，只要让乒乓球在向前运动的时候同时下旋，例如按住中后部“搓”出去，只要力度足够就能发生，例如下图：



来自上述推送文章

一、力学原理与程序设计




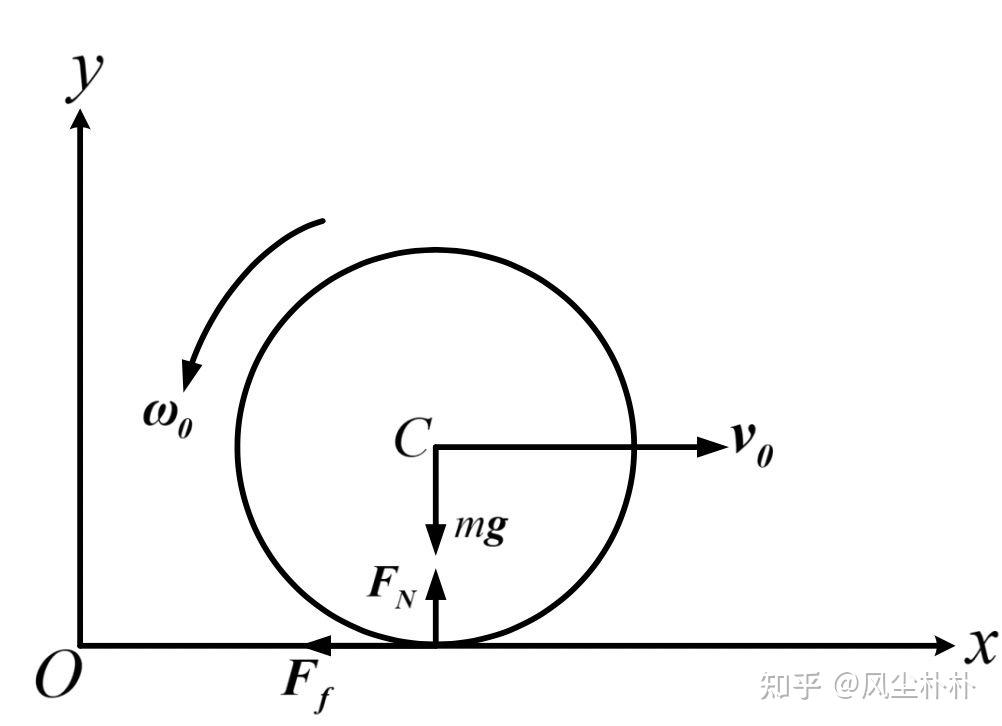
来自上述推送文章

考虑一维的平动，即乒乓球现折x轴方向平动，不发生碰撞和“起跳”，质地均匀，则过质心的一个截面如图。
开始运动时必然处于滑动摩擦状态，运动公式可以写为：（ v_0 其中为初速度， \omega_0 为初角速度， m 为质量， R 为半径，摩擦因数 \mu ）
\begin{cases} m\frac{d^2x_c}{dt^2}=-F_f &, F_f=\mu mg \\  J_c\frac{d^2\varphi}{dt^2}=-F_fR  &, J_c=\frac{2}{3}mR^2 \end{cases} 从而得到 \left\{\begin{array}{l} \frac{\mathrm{d} x_{C}}{\mathrm{~d} t}=v_{0}-\mu g t \\ \frac{\mathrm{d} \varphi}{\mathrm{d} t}=\omega_{0}-\frac{3 \mu g}{2 R} t \end{array}\right. 及 \left\{\begin{array}{l} x_{C}(t)=v_{0} t-\frac{1}{2} \mu g t^{2}+R \\ \varphi(t)=\omega_{0} t-\frac{3 \mu g}{4 R} t^{2} \end{array}\right.
从运动学角度出发，在摩擦力作用下，质心速度和角速度减小，如果速度先减少为0，则发生回旋，若角速度先至0，则向前运动，若同时至0，则恰好停止运动。以下给出盘底判定条件：
若先停止平动，由 \frac{dx_c}{dt}=0 ，得到 t_1=\frac{v_0}{\mu g} 。若先停止滚动，由 \frac{d\varphi}{dt}=0 ，得到 t_2=\frac{2R\omega}{3\mu g} 。
（1）当 t_1=t_2 时，打滑后恰好停止；
（2）当 t_1>t_2 ，先停止转动（角速度为0，速度尚未至0），继续打滑前行（开始向上旋转），角速度增加，速度继续减小，直到发生纯滚。设 t_3 时发生纯滚，
则 v_0-\mu gt_3=R\frac{d^2\varphi}{dt^2}\left(t_3-t_2\right) 得到 t_3=\frac{2\left(R\omega_0+v_0\right)}{5\mu g} ，
（3）当 t_1<t_2 ，发生回旋（仍在打滑）,之后速度反向从0开始增大，角速度减小直到发生纯滚。
同理设 t_3 时发生纯滚，有 \mu g\left(t_3-t_1\right)=R\left(\omega_0-\frac{3\mu g}{2R}t_3\right) ，结论同上。
发生纯滚时，速度和角速度满足： \frac{\mathrm{d} x_{C}}{\mathrm{~d} t}=-R \frac{\mathrm{d} \varphi}{\mathrm{d} t}
二、Matlab实现

2.1运动学求解

首先输入初始化条件：
v0=20;%m/s
w0=5*pi;%rad/s
u=0.9;
R=1;%m
g=9.8;
T=3;%预设需要观察的总时长/s第二步判断运动类型
tp1=v0/(u*g);
tp2=2*w0*R/(3*u*g);
if tp1<tp2
    fprintf('在%.2fs时，位移%.2fm，开始回旋\n',tp1,v0*tp1-0.5*(u*g)*tp1*tp1+R);
elseif tp1==tp2   
    fprintf('在%.2fs时，位移%.2fm，恰好停止\n',tp1,v0*tp1-0.5*(u*g)*tp1*tp1+R');
else
    fprintf('在%.2fs时，位移%.2fm，开始向前滚动\n',tp2,v0*tp2-0.5*(u*g)*tp2*tp2+R');
end第三步：根据初始化参数，判断观察时长，是否仅观察滑动，最后输出观察期间内球心位移xc1，角度变化th1
tp=2*(R*w0+v0)/(5*u*g);%tp前为滑动，之后为纯滚
%调用子函数
    tp=T;
end
t1=0:0.001:tp;
t1=t1';
[xc1,th1,vc1,w1]=slide_go(v0,w0,u,g,R,t1);此处的子函数为：
function [xc,th,vc,w]=slide_go(v0,w0,u,g,R,t1
    xc=v0*t1-0.5*u*g*t1.*t1+R;
    th=w0*t1-(3*u*g)/(4*R).*t1.*t1;
    vc=v0-u*g.*t1;
    w=w0-(3*u*g)/(2*R).*t1;
end如果预设时间足够长，会发生纯滚
if T>tp
    t2=0:0.001:T-tp;%从纯滚发生开始计时
    t2=t2';
    [xc2,th2,vc2,w2]=only_roll(vc1(end),w1(end),xc1(end),th1(end),t2);%纯滚
    xc1=[xc1;xc2];%扩展位移向量
    th1=[th1;th2];
    vc1=[vc1;vc2];
    w1=[w1;w2];
    t1=0:0.001:T;%总的时间向量
end此处的计算纯滚子函数为：
function [xc2,th2,vc2,w2]=only_roll(v1,w1,xc1,th1,t2)
xc2=xc1+v1*t2;
th2=th1+w1*t2;
vec=ones(length(t2),1);
vc2=v1*vec;
w2=w1*vec;
end第五步：为了观测速度和位移量，绘制曲线图显示
subplot(3,3,1);
plot(t1,xc1,'-b',t1,th1,'-k','LineWidth',2);
legend('球心位移','转角');
subplot(3,3,4);
plot(t1,vc1,'-b','LineWidth',2);
legend('球心速度');
subplot(3,3,7);
plot(t1,w1,'-k','LineWidth',2);
legend('角速度');最后，用一个函数来做显示化的部分
subplot(1,2,2);
moive_figure(xc1,0,th1);接下来主要介绍一下可视化函数这部分
2.2可视化

一个疑问：原文中在逐帧显示时，通过pause暂停实现时间间隔，但是循环中每次绘图时间不统一，且无法确定，并不能让显示的情况和实际运动状态相符合，所以我在计算结束后保存一个avi文件，将帧率和显示步长相统一。
函数的输入function moive_figure(xc,zc,th)
          ...
          end第一步：利用坐标系转换生成构成球面的点
[ps,ts]=meshgrid(linspace(0,2*pi,100),linspace(0,pi,100));
xs=cos(ts);
ys=sin(ts).*cos(ps);
zs=sin(ts).*sin(ps); 第二步：对于视频文件的创建
mov=VideoWriter('乒乓球回旋3');
mov.FrameRate=1000;%
open(mov);%打开
for i=1:100%根据具体帧数设置
...
   h=getframe(gcf);
   writeVideo(mov,h);
...
end
close(mov);%给关闭
第三步:for循环内逐帧显示图像
[x1,yl,zl]=rotter(0,zc,xs,ys,zs,th(i));
mp=xs.^2+ys.^2-zs.^2;
surf(x1+xc(i),yl,zl,mp);%四维画图，？？
axis image;axis([-1 10 -1 1 -1 1]);
shading interp;
%pause(0.001);%程序暂停0.001s---原文做法，也可能时我哪里理解不对
drawnow;第四步：对于余弦变换矩阵可以用下列的子函数实现（余弦变换的介绍部分参考推送文章）
function [xs,ys,zs]=rotter(xc,zc,x,y,z,th)
        xs=xc+cos(-th)*(x-xc)+sin(-th)*(z-zc);
        ys=y;
        zs=zc-sin(-th)*(x-xc)+cos(-th)*(z-zc);
end2.3一个结果



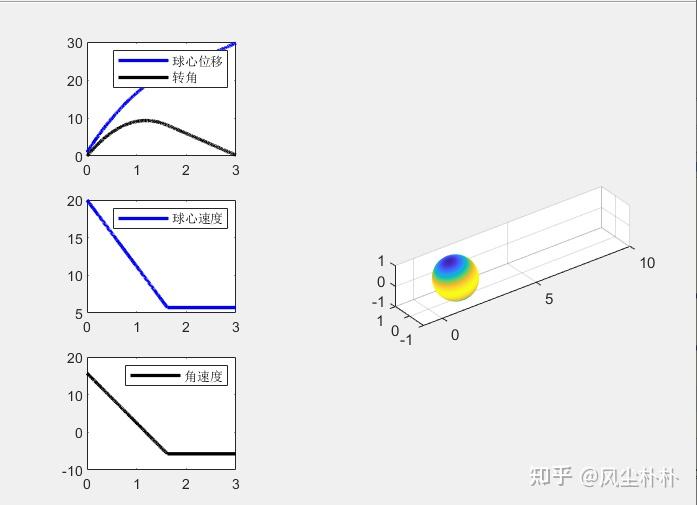
三、GUI练习实践

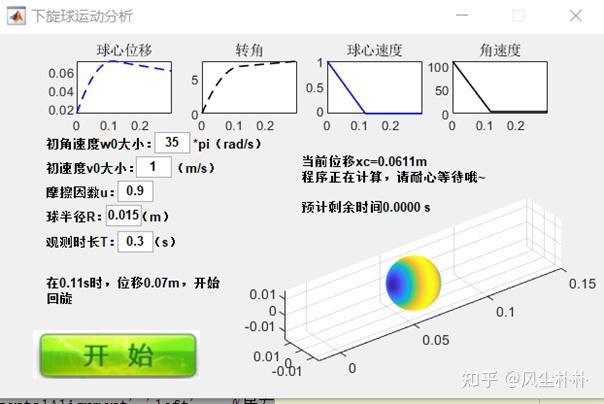
最后，做成了一个GUI截面，可以输入初始条件，如下展示


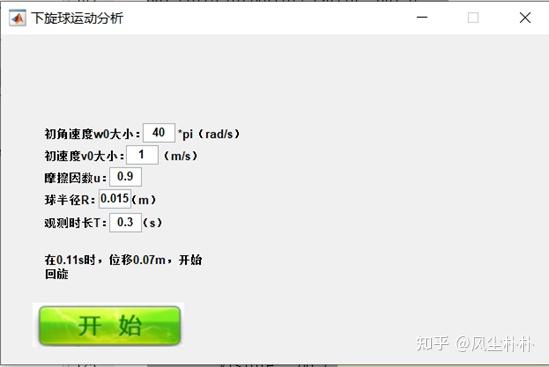
之后点击开始—显示初始条件下位移，转角以及速度曲线，打印判断结果，何时发生纯滚，是继续向前还是回旋还是恰好停止。并开始计算，实时反映当前位移和剩余时间。


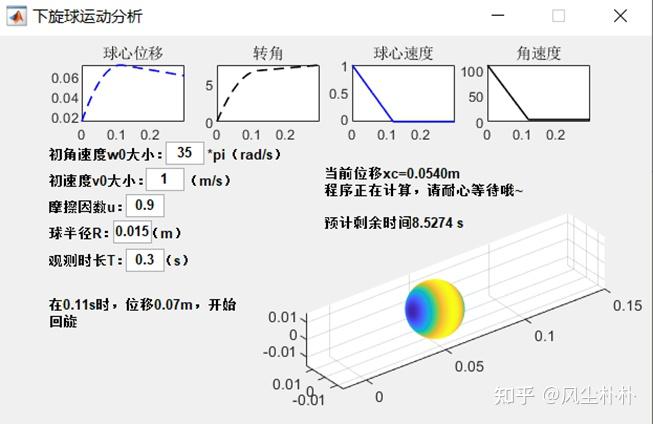
程序结束时，“开始”按钮重新显示出来，同时生成对应的视频文件。


当然，这部分也做了一些改进，有机会再写吧。
同时，我希望下一步考虑非理想的滚动状态，曲线和视频的互动，比如加入视频的滚动条和倍速播放，以及二维情况等等。作为初学者，一定有许多不足的地方，欢迎小伙伴们交流讨论~

青瓷器

站位支持

前恶后善也有罪

无论是不是沙发都得回复下